This surface wave-resolving numerical model is simulating the performance of a network of frictional mass units in a channeled wave-tank environment. This model was one of our earliest methods for physical simulation; subsequent physical prototyping and wave tank experiments have allowed us to compare the model behavior with multiple laboratory-observed conditions and tune its accuracy. In other words, the physical dynamics shown here are true to the way an eight-row network of actual marine biomass units would affect regular waves of 2-foot height and 6-foot wavelength—the wave formation would diffract as shown, and overall wave energy would be reduced by over 70%. By adjusting the input parameters of the simulation, such as wavelength and network configuration, along with N = 44, 99, and 374 units and the mass of the individual units being varied, the model is able to calculate corresponding conditions of the resultant wave behavior as it reacts to the different configurations. This allows us to test the behaviors of large networks composed of non-uniform unit types with unique sizes and configurations.
What we learned
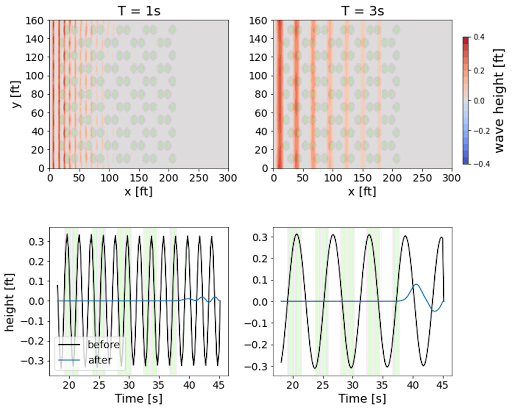
In creating this model and observing how the simulated waves interact with a simulated unit network, we were able to generalize the reactive properties of the marsh mat network that produce the wave dampening effect. Through validation from the Wave Tank Lab Tests, we confirmed that with enough rows, a floating network of units can progressively dampen any wave. We also found that the unit spacing affects damping properties, with tighter networks more effective at damping incoming waves. Diversifying the size of the mats also improved damping efficacy, but was not as impactful as the network spacing.
Numerical-Physical Model Verification
To create a mathematical representation of the floating unit network in this simulation environment, we first guessed at physical fluid properties (increased density, viscosity, and drag constants) that we thought would represent our vegetated mat network. Then, after our 44-unit prototype network was built in the wave lab in Summer 2021, we were able to reverse-engineer more accurate physical fluid properties from observed physical performance in the lab. To put our assumptions and numerical representation techniques to the test, we used our research from the wave tank experiments conducted at the O.H. Hinsdale Wave Tank Research Facility to verify results through our many trials with different network configurations and wave types. Proving that our numerical model can accurately reproduce the observed network behavior in any wave condition is a critical step in confidently showing the efficacy of a given network in situ.


About the model
This model was developed using fluid surface-resolving mathematics (Navier-Stokes shallow water equations, Boussinesq approximations, and a finite-difference scheme) and was run on a supercomputer.
The Navier-Stokes Shallow Water Equations
The Navier-Stokes shallow water equations are cornerstone equations in fluid dynamics which represent Newton’s Conservation of Momentum and Conservation of Mass laws for Newtonian fluids. Newtonian fluids, such as seawater or molasses, have a constant viscosity at a constant temperature. Integrating these partial differential equations in a shallow-water context removes the vertical velocity (Z-direction) term, assuming that the scale of the vertical velocity is small compared to the horizontal velocity scale. This set of numerical methods—tuned for nearshore ocean conditions and optimized for computation—enables us to accurately model the hydrodynamic interactions between morphologically-complex Nature-Based Infrastructure and water.
The Boussinesq approximations
The Boussinesq approximations assume that variations in fluid density are so small that they have no effect on the flow field except to provide buoyancy forces. This assumption allows for the elimination of the vertical variable from the Navier-Stokes flow equations while still maintaining influences of the vertical structure. In doing so, the model is now able to incorporate dispersion effects which better represent wave propagation.
Finite-Difference Scheme
Finite-Difference Scheme is a method for computing the above fluid modeling numerical equations. This method is more flexible than the alternatives (spectral, pseudospectral) and is able to handle varying coefficients, differing boundary conditions, and irregular geometries—although it is more complex to set up the model. These features make it suitable for the irregularities of coastal shorelines and Nature-Based Infrastructure.